 Index
Index

Numerology derives occult and esoteric relationships between numbers and physical objects or living things. People who believe in numerology claim that numbers govern much of what happens in relationships, health, finances, and life in general.

| Name: |
|
| Birth Date: |
Format: MMDDYYYY |
The numbers derived from a person's name and date of birth may be used to calculate a numerology chart about personality, relationships, and even the future. There is no scientific proof that any of the claims made by numerologists are true, but this does not stop people from believing or being interested in the insights that numerology can give them. This page generates free numerology readings using a numerology calculator. Use the name and date in your birth certificate.
Numerology originated approximately in one thousand BCE when Roman and Hebrew numbers consisted of letters of the alphabet and the number zero had not yet been invented. Some of the numbers formed by letters were interpreted as words whose meaning could be scrutinized for mystical insights. Even today, some Roman numbers can be associated with English words and meanings. For example, 1009 (Roman: MIX) is an English verb and noun, 100 (Roman: C) is pronounced like SEE or SEA, 59 (Roman: LIX) is pronounced like LICKS or LIKES, and 40 (Roman: XL) is an abbreviation for EXTRA LARGE or is pronounced like EXCEL. These numerolinguistic associations can lead to many connotations.
| Numeral Systems | ||||||||||
| Western Arabic | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Eastern Arabic | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| Chinese numbers | 〇 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 |
| Hebrew numbers | א | ב | ג | ד | ה | ו | ז | ח | ט | |
| Roman numbers | I | II | III | IV | V | VI | VII | VIII | IX | |
The modern Chinese numerals have a normal form, illustrated above, and a financial form that makes it more difficult to alter a document, such as changing the number two to a three by adding a line. The Babylonians were the first to use the number zero as a place holder in the 3rd century BCE. The concept of zero as a number and not merely a symbol for separation was used in India by the 9th century CE. The use of the number zero and Arabic mathematics was popularized in Europe during the 11th century CE by the Italian mathematician Fibonacci. Learn about Fibonacci's problem of the birds.

After the adoption of the Arabic number system, many numerology systems were developed to assign numerical values to the letters of the alphabet. The system known as gematria, which was originally developed for the Hebrew alphabet, computes values for words by adding the values of the letters. Words which have the same numerical equivalence are thought to share some occult connection. In contemporary terms, gematria corresponds to a hash function[1], and the numerical equivalence of two words is called a hash code collision. The following table illustrates a simple mapping of the English alphabet to numerical values. The characters of a word are substituted with the corresponding numbers, and the numbers are then added together to get the numerical value of the word.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A, J, S | B, K, T | C, L, U | D, M, V | E, N, W | F, O, X | G, P, Y | H, Q, Z | I, R |
A passage in the Book of Revelation (13:18) of the New Testament says that a person who has understanding can calculate that 666 is the number of the beast, and that the beast is a man. Biblical scholars have tried to identify the man using Greek isopsephy and Hebrew gematria, where every letter corresponds to a number. Some theologians support the interpretation that the name and title of Nero Caesar who was a Roman Emperor from 54 to 68 CE transliterates to the Hebrew letters that map to 666.[2]
Here is wisdom. Let him who has understanding calculate the number of the beast, for the number is that of a man; and his number is six hundred and sixty-six. (Revelation 13:18, New American Standard Bible, 1995)

The English Qabalah uses the following numeric correspondences:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| A | L | W | H | S | D | O | Z | K | V | G | R | C |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| N | Y | J | U | F | Q | B | M | X | I | T | E | P |
The original order of the English Qabalah system (A,L,W,H,...) was developed by counting every 12th letter in the English alphabet and upon reaching the end of the alphabet, continuing at the beginning again. However, this is equivalent to mapping the letters of the English alphabet to the positions corresponding to
where Xn is the position of the next letter and Xc is the position of the current letter. Thus, if A starts in position 1, B should be in position 1+19 = 20. Then, C should be in position 20+19 = 39, which modulo 26 becomes 13, and so on. Since 19 is a prime number, the 26 slots are filled without overlaps. This is similar to a perfect hash function that maps distinct elements to integers with no collisions.
The date of birth is used to calculate the Life Path number. The month, day, and year are added together to arrive at a total. The resulting four-digit number is reduced by adding its digits. The process is continued until a single digit is obtained. For example, the calculation for a person born on November 7, 1973 would be obtained by adding 11+7+1973 to obtain 1991. Adding the digits 1+9+9+1 we get 20 which when added as 2+0 reduces to the Life Path number 2.
Sexagesimal (base 60) numbers
Have you ever wondered why an hour has 60 minutes and a circle has 360 degrees?
The base 60 system was developed between 3000 BC and 2000 BC by the Sumerians
who lived in southern Mesopotamia (now Iraq) during the Early Bronze Age.
The number system was passed down to the ancient Babylonians and we still use it
today for telling time and measuring angles. One hour has 60 minutes,
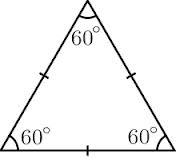
and one minute is divided into 60 seconds. An equilateral triangle has three
equal angles of 60 degrees. The sum of the angles of any triangle add to 180 degrees,
which is 3×60. A hexagon can be constructed by placing six equilateral triangles
so that they share one vertex. Thus, a circle circumscribing the hexagon has 360 degrees which is 6×60.
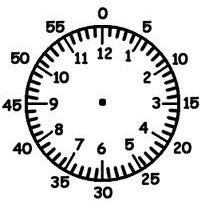
Clock faces with the numbers 1 to 12 spaced every 5 minutes are very familiar today,
where 5 minutes on the clock face correspond to an angle of 30 degrees.
The number 60 was favored by
the ancient civilizations because it is evenly divisible by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60.

Linguistic oddities
One would expect that numbers would be a universal language, but the graphic representation and
oral expression of the numbers differs across the world.
The United States uses periods as decimal separators and commas to separate thousands, e.g., 12,341.34,
whereas most of Europe, South America and former French and Portuguese colonies use the reverse, e.g., 12.341,34.
The number 71 in English is pronounced "seventy one", whereas in German it is pronounced einundsiebzig, which means "one and seventy."
French is even stranger because 71 is soixante et onze, which means "sixty and eleven"; 80 is quatre-vingts,
which means "four-twenties", and 90 is quatre-vingt-dix, which means "four-twenty-ten."
Counting in twenties was common in the United States during the 19th century. Abraham Lincoln started his Gettysburg Address with these words:
"Four score and seven years ago ..." That is not too different from the way 87 is expressed in French.
Modern Computers and Numbers
Computers can only handle binary numbers (0 and 1) called bits. These bits are
grouped in sets of 8 to represent numbers from 0 to 255, or in sets of 16 to represent numbers from 0 to 65,535.
Any alphabetic representation must consist of a mapping of these numbers to specific graphic characters.
Each set of mappings is called a Code Page. Thus, a Latin code page maps 256 eight-bit
numbers into graphic characters for Western European languages, whereas a Slavic code page
maps the same 256 numbers into Cyrillic characters for Russian and Bulgarian.
Unicode is a 16-bit code that provides mappings for the characters of over 90
alphabets, and UTF-8 is a reversible encoding mechanism that stores
Unicode characters as 8-bit codes, but some characters require a sequence of several 8-bit codes.
In the UTF-8 code and in the ASCII code, the upper case
characters A through Z correspond to the numbers 65 through 90, whereas the lower case
characters are mapped from 97 through 122. We could call this mapping the Computer Qabalah
with which many electronic messages can be decoded.
The system most commonly used in our day-to-day computations is the decimal or base 10 system. This counting system evolved naturally because we have 10 fingers. The use of computers has made it necessary to work with number systems whose bases are powers of two. The hexadecimal (base 16) system uses the digits 0 through 9 and the letters A through F as the numeric symbols. Figure 1 displays the upper case letter C as hexadecimal 43, which corresponds to the decimal number 67. The conversion from hexadecimal to decimal is done by multiplying the value of the first hex digit times 16 and adding the value of the second hex digit. Thus, 4×16+3 = 67.


Pseudorandom numbers
In modern times, the study of the relationships between words and numbers has increased,
specially for the purpose of encrypting data. Some simple systems like the calculator
spelling illustrated in Figure 2 are only for entertainment, but modern cryptography
combines the use of pseudorandom number generators with modular arithmetic to
map any text into apparent gibberish.
The equation Xn = (Xc+19) modulo 26, discussed
above, is an example of a simple pseudorandom number generator.
The only way to decode messages with this type of encryption
is to know the sequence of numbers generated by the pseudorandom number generator.
Numerical encryption of messages
To encode a message using pseudorandom numbers we
assign each letter of the alphabet a value from 1 to 26, so that a=1, b=2, etc.
Now, consider a pseudorandom number generator that produces: 1, 19, 12, 5, 24, 17, etc.
The letters of the original message are encoded by adding the value of each letter
to its corresponding pseudorandom number in the sequence, and then applying a modulus operation
to map the resulting sum back to a letter.
The following table illustrates how the word "secret" becomes "txomck" using this encoding procedure.
Notice that unlike simple substitution ciphers, the letter "e" is mapped to different letters
because each instance is encoded with a different pseudorandom number value.
Decoding the message requires knowing the sequence of numbers that were used
to encode the message which is very difficult for sophisticated pseudorandom number
generators.
| Original message | s | e | c | r | e | t |
| Letter value | 19 | 5 | 3 | 18 | 5 | 20 |
| pseudorandom number | 1 | 19 | 12 | 5 | 24 | 17 |
| Value plus number (Mod 26) | 20 | 24 | 15 | 23 | 3 | 11 |
| Encoded message | t | x | o | m | c | k |
Note: The information entered above is used exclusively for the calculations and it is not saved in any form.
The word qabalah is often spelled as kabbalah, kabbala, kabala, cabbalah, cabbala or cabala.
The Life Path information is derived from Michael McClain, Astrology-Numerology.com. Used with permission.