 Index
Index

 The Astronaut's Pee
The Astronaut's PeeAn astronaut orbiting in a space capsule at normal atmospheric pressure ejects 100 grams of water into the vacuum of space. How much water will turn into ice?
The problem gives us the hint that water will freeze in space. Looking at the phase diagram for water, we can see that below a pressure of 0.006 atmospheres (611.7 Pascals) water cannot exist in the liquid state. In the vacuum of space, water can only be gaseous or solid. Any liquid water ejected into space will boil, and the evaporation will cool some of the remaining water below the freezing point.
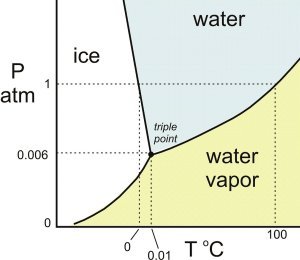
The heat for melting or freezing water, also called the Heat of Fusion, is 80 calories per gram at 0°C. It is necessary to remove 80 calories of energy to freeze one gram of water at 0°C. The heat for boiling or condensing water at 100°C, called the Heat of Vaporization, is 539 calories per gram. The following graph summarizes the effect of energy on the temperature of water in its solid, liquid, and gaseous phases.

Since the problem does not state the temperature of the water ejected into space,
we can do the calculations for 0°C and for 100°C, which are the minimum and
maximum temperatures for water at normal pressure within the space capsule.
We can solve the problem as follows:
Let X be the amount of water that evaporates, and 100-X the amount of
water that turns into ice.
For water at 0°C, we can set up the following equation, where (100-X) 80 is the number of calories required to freeze 100-X grams of water at 0°C, and 539 X is the number of calories removed by the evaporation of X grams of water.
(100 - X) 80 = 539 X
X = 8000/619 = 12.9 grams
If the ejected water has a temperature of 0°C, only 12.9 grams need to evaporate to freeze the remaining water (87.1 grams).
For water at 100°C, it is first necessary to reduce the temperature to 0°C. This requires 100 calories per gram. In addition, 80 calories are required to freeze one gram of water. Thus, we need to remove 180 calories to freeze 1 gram of water at 100°C. We can set up the following equation, where (100-X) 180 is the number of calories required to freeze 100-X grams of water at 100°C, and 539 X is the number of calories removed by the evaporation of X grams of water.
(100 - X) 180 = 539 X
X = 18000/719 = 25.0 grams
For water ejected into space, 87.1 grams turn into ice if the water is initially at 0°C, and 75.0 grams turn into ice if the water is at 100°C. Thus, at least 75 grams out of the original 100 grams or 75% will turn into ice.
The idea for this puzzle originated from the following 1976 transcript of astronaut Russel Schweickart talking to Peter Warshall about waste disposal in space:
Schweickart: Well, actually, in Skylab we did something similar to that. But on Apollo the urine then would go outside, and you'd have to heat the nozzle because, of course, it instantly flashes into ice crystals. And, in fact, I told Stewart this, the most beautiful sight in orbit, or one of the most beautiful sights, is a urine dump at sunset, because as the stuff comes out and as it hits the exit nozzle it instantly flashes into ten million little ice crystals which go out almost in a hemisphere, because, you know, you're exiting into essentially a perfect vacuum, and so the stuff goes in every direction, and all radially out from the spacecraft at relatively high velocity. It's surprising, and it's an incredible stream of ... just a spray of sparklers almost. It's really a spectacular sight. At any rate that's the urine system on Apollo.
This phenomenon may also be responsible for the Younger Dryas cooling event 12,900 years ago. Read more about this.